Nykypäivän peruskoulussa pyritään pienentämään eri oppiaineiden välisiä
kuiluja integroimalla oppiaineiden sisältöjä laajemmiksi kokonaisuuksiksi.
Monien koulujen opetussuunnitelmissa mainitaankin oppiaineiden välinen
yhteistyö ja aihekokonaisuuksien käsittely yli oppiaineiden rajojen.
Niinimäki Katja 129711
Matematiikkaa peruskoulun tekstiilityön tunnilla
Essee matematiikan sivuainelaudaturiin 1 ov
Joensuun yliopisto
Tekstiilityön opettajan koulutus
Kesäkuu 2000
1 Yleistä
Nykypäivän peruskoulussa pyritään pienentämään eri oppiaineiden välisiä
kuiluja integroimalla oppiaineiden sisältöjä laajemmiksi kokonaisuuksiksi.
Monien koulujen opetussuunnitelmissa mainitaankin oppiaineiden välinen
yhteistyö ja aihekokonaisuuksien käsittely yli oppiaineiden rajojen. Ihan-
teellista mielestäni olisikin, jos peruskoulu voisi tarjota opetusta monipuo-
lisesti. Käytännön elämässähän ei ole olemassa eri ”oppiaineita”, vaan
opittuja tietoja ja taitoja on pystyttävä soveltamaan sekaisin yli perinteis-
ten oppiainerajojen.
Jokainen oppilas tietää, että matematiikkaa tarvitaan aivan jokapäiväisis-
sä asioissa kuten vaikkapa rahaa käytettäessä. Mutta matematiikkaa ja
matematiikan kautta opittuja tietoja tarvitaan myös monessa sellaisessa
asiassa, minkä ei heti luulisi liittyvän matematiikkaan millään lailla. Äkki-
seltään luulisi matematiikan ja tekstiilityön olevan kovinkin kaukana toisis-
taan, sillä tekstiilityöhän kuuluu taito- ja taideaineisiin ja matematiikka
teoreettisiin oppiaineisiin. Tekstiilitöissä matematiikkaa löytyy kuitenkin
aina, olipa kyse mistä käsityötekniikasta tahansa. Muutama oppilas onkin
tekstiilityön tunnilla opettajana ollessani tuskaillut, että pitääkö täälläkin
olla näin paljon matikkaa. Siellä siis oppilaatkin huomaavat matematiikkaa
tarvittavan paljon muuallakin kuin matematiikan tunnilla. Matematiikassa
opitut asiat saavat näin käytännönläheisiä esimerkkejä ja tulevat lähei-
simmiksi oppilaille.
Tekstiilitöissä oppilaan eteen tulee laskutoimitusten ja matemaattisten kä-
sitteiden lisäksi runsaasti ongelmanratkaisua ja loogista päättelyä vaativia
työvaiheita. Nämä molemmathan ovat tärkeitä matematiikan kautta opit-
tavia taitoja käytännönelämää varten. Peruskoulun opetussuunnitelman
perusteissa (POPS 1996, 77) mainitaan matematiikan opetuksen keskei-
siksi tavoitteiksi, että oppilas oppii käyttämään matematiikkaa monipuoli-
sesti jokapäiväisessä elämässä, osaa käyttää matematiikkaa apuna on-
gelmanratkaisussa ja oppii päättelemään asioita johdonmukaisesti ja sel-
keästi. Tekstiilityön ja matematiikan integrointi käy siis aivan luonnostaan,
vaikkei sitä aina havaitakaan.
Mielestäni tekstiilityö ja matematiikka sopivatkin oikein hyvin samalle
opettajalle, vaikka moni tällaista yhdistelmää kummasteleekin. Matema-
tiikkaa hallitseva tekstiilityön opettaja osaa käyttää oikeita matemaattisia
termejä opettaessaan tekstiilityön tunnilla tarvittavia laskutoimituksia.
Näin oppilaiden on helpompi soveltaa matematiikan tunnilla oppimaansa
tietoa käytäntöön ja he saavat konkreettisia esimerkkejä matematiikan
käytöstä. Jos asioista puhutaan tekstiilityön tunnilla eri nimillä, tuntuu tu-
tutkin asiatkin oppilaista vaikeilta. Oppilaiden on helpompi oppia uutta tie-
toa, kun he voivat rakentaa sen aiemmin opitun varaan. (Seppälä 1994,
12).
2 Laskutoimituksia tekstiilityössä
Matematiikkaa on kaikkialla, ainakin tekstiilityön tunnilla. Kaikkia perus-
laskutoimituksia tarvitaan välttämättä. Jokainen vähänkin käsitöitä tehnyt
tietää, että töiden ohjeet sisältävät erilaisia lukuja pilvin pimein. Tekstiili-
työn tunnilla voi huomata prosenttilaskua tarvittavan muuallakin kuin
kaupassa alennusmyyntihintoja laskettaessa. Ilman mittaamisen taitoa-
kaan ei tekstiilityön tunnilla tule toimeen. Ja eipä vielä riitä, että osaa mi-
tata mittanauhalla senttimetrejä, vaan täytyy hallita myös muut mittayk-
siköt ja niiden muunnokset.
Peruslaskutoimituksia eli yhteen-, vähennys-, kerto- ja jakolaskuja tarvi-
taan kaikista eniten. Oppilaille täytyy neuvoa esimerkiksi, kuinka laske-
taan villasukkaan tai lapaseen tarvittavien silmukoiden määrä silmukkati-
heyden avulla. Jo pelkän sukan silmukoiden määrän laskemiseen tarvitaan
kaikkia peruslaskutoimituksia. Jos sukkaan tehdään vielä kirjoneulekuvio-
ta, täytyy laskea että silmukkamäärä on jaollinen mallikerran silmukka-
määrällä. (Karhu 1996, 21, 22, 27). Monesti oppilaat laskevat tekemänsä
työn kustannukset, jolloin tulee peruslaskutoimitusten lisäksi vertailua
kannattavuudesta.
Prosenttilaskujakin tarvitaan yllättävän paljon. Oppilaille täytyy opettaa
prosenttikäsite viimeistään siinä vaiheessa kun ommellaan vaatteita. Esi-
merkiksi housuihin tarvittavaa kangasmäärää laskettaessa täytyy ottaa
huomioon, että kangas kutistuu pituussuunnassa, kun se kastellaan en-
simmäisen kerran. Kangasta tuleekin ostaa 5 % enemmän, jotta se riittäi-
si housuihin myös kutistamisen jälkeen.
Kankaiden tai lankojen värjäämisessä prosenttilaskut ovat värjäyksen on-
nistumisen kannalta pakollisia. Käytettävän väriaineen määrä lasketaan
prosentteina värjättävän materiaalin massasta. Esimerkki. Kangasta on
500 grammaa. Jauhemaista väriainetta tarvitaan 3,5 % kankaan massas-
ta.
Mittakaava ja suhdeluvut tulevat myös esiin käsitöiden ohjeissa. Värjättä-
essä kangasta tarvittavan veden tai nestemäisen väriaineen määrä laske-
taan suhteutettuna kankaan määrään. Esimerkki. 100 grammaa kangasta
kohti tarvitaan väriliemeen1,5 litraa vettä ja 10 millilitraa nestemäistä vä-
riainetta. Kuinka paljon tarvitaan vettä ja väriainetta 400 grammaa paina-
van kankaan värjäämisessä.
Mittakaavan käyttöön löytyy myös esimerkki tekstiilityön tunnilta. Vaattei-
den kaavoja piirrettäessä saattaa törmätä 1:4 kaavoihin. Kaava saattaa
siis lehden ohjeessa olla piirrettynä neljäsosaan luonnollisesta koostaa.
Tällaiseen mittakaavaan on tekstiilityön luokassa olemassa apuvälinekin;
viivoitin, jonka jokainen sentti on jaettu neljään pikkusenttiin.
Kaikkea ei kuitenkaan voi tekstiilitöissäkään tarkkaan laskea, vaan arvi-
ointia joutuu käyttämään hyväkseen moneen otteeseen työn edetessä.
Varsinkin langan määrää joutuu arvioimaan usein, sillä aina ei voi sanoa,
minkä pituinen langanpätkä riittää tietyn värisen raidan tekemiseen vil-
lasukan varteen. Myös monissa ohjeissa tarvikkeiden määrät ilmoitetaan
noin määrinä.
Mittaaminen kuuluu olennaisesti tekstiilityöhön ja onhan mittanauha yksi
perustyövälineistä tekstiilityön tunnilla. Mittaamisen tarkkuus riippuu pal-
jon tehtävästä työstä. Tekstiilityössä moni oppilas oppii mittaamisen tark-
kuuden tärkeyden kantapään kautta. Esimerkiksi epätarkasti mitattujen
kangaspalojen ompeleminen yhteen on vaikeampaa kuin tarkkaan mitat-
tujen. Jos mittausvirhe toistuu monta kertaa voi lopputulos olla aivan eri
kuin mitä oli suunniteltu.
Mittaamisen seurauksena oppilaat joutuvat käyttämään eri mittayksikköjä.
Yleisimmin käytetty yksikkö on senttimetri, mutta tutuksi tulevat varmasti
myös millimetri ja metri. Massan yksiköitä tarvitaan myös, sillä lankojen
määrät ilmoitetaan lähes aina grammoina. Pinta-alan yksiköitä tarvitaan
harvemmin, mutta eivät nekään aivan kummajaisia ohjeissa ole. Tilavuu-
den yksiköistä käytetään yleisimmin litroja, desilitroja ja millilitroja.
3 Geometriaa tekstiilityössä
Geometria on ehkä eniten tekstiilityössä käytetty matematiikan osa-alue.
Tekstiilityö vaatii paljon geometrista ajattelua ja hahmottamiskykyä. Mo-
net perinteiset käsityöt on kuvioitu juuri geometrisin kuvioin. Tilkkutyöt
ovat matemaattisesti mielenkiintoisia, sillä ne perustuvat eriväristen geo-
metristen kuvioiden yhdistämiseen. Yleisimmät tilkkutyömallit muodostu-
vat suorakulmioista ja neliöistä.
Geometriaa apuna käyttäen monesta tekstiilityön tunnilla vastaan tulevas-
ta ongelmasta selviää yllättävän yksinkertaisella ratkaisulla. Kaikki eivät
kuitenkaan löydä noita geometrisia muotoja ja huomaa millaisista osista
kappaleet tai kuviot muodostuvat. Tekstiilityön tunnilla joutuukin välttä-
mättä neuvomaan oppilaille geometrista ajattelua ja geometristen muoto-
jen hyödyntämistä.
Suoraan törmää kaikkialla ja viivoitin onkin paljon käytetty apuväline var-
sinkin kaavoja piirrettäessä. Suorien yhdensuuntaisuutta hyödynnetään
esimerkiksi kankaiden leikkaamisessa. Jotta housunlahkeet eivät kiertäisi,
täytyy housujen kappaleet leikata kankaasta lankasuoran mukaisesti.
Kaavoihin on aina merkitty lankasuora, jonka täytyy olla yhden suuntai-
nen kankaan reunan kanssa kaavoja kankaalle aseteltaessa.
Symmetriaa löytyy varsinkin perinteisistä kirjontakuvioista. Vanhoissa vil-
lakankaalle kirjotuissa rekipeitoissa monimutkaiset kuvioit ovat joko kes-
kipisteensä tai keskipisteen kautta kulkevien suorien suhteen symmetrisiä.
Symmetriaa löytyy runsaasti myös tilkkutyömalleista ja neuleiden kuvi-
oinnista. Tilkkutöitä tarkasteltaessa löytyy runsaasti malleja, jotka koos-
tuvat yhtenevistä kuvioista.
Kolmiulotteisuus on mukana lähes kaikessa, mitä tekstiilitöissä tehdään-
kin. Esimerkiksi vaatteita ommeltaessa tasona olevasta kankaasta saa-
daan kolmiulotteinen tuote. Tekstiilitöissä oppilailta vaaditaankin avaruu-
dellista hahmottamiskykyä, sillä ymmärtääkseen mitä on tekemässä, täy-
tyy oppilaan osata hahmottaa millainen kangaspala vastaa esimerkiksi
housujen etukappaletta. Oppilas joutuu työn edetessä monesti hahmotta-
maan, millainen tuote on valmiina.
Työohjeita lukiessa tulee eteen hahmottamiskyvyn tarpeellisuus. Kun oh-
jeessa on kuva, on osattava löytää sama vaihe omasta kolmiulotteisesta
työstään.
Neliö on varmasti käytetyin geometrinen muoto tilkkutöissä. Neliötä yh-
distellään usein myös suorakulmaisiin kolmioihin. Omia tilkkutyömalleja
suunniteltaessa oppilaiden onkin helppo lähteä liikkeelle neliöistä, joista
saadaan lävistäjillä suorakulmaisiksi kolmioiksi. Neliö saadaan myös jaet-
tua suorakulmioiksi ja pienemmiksi neliöiksi. (Karhu 1996, 207)
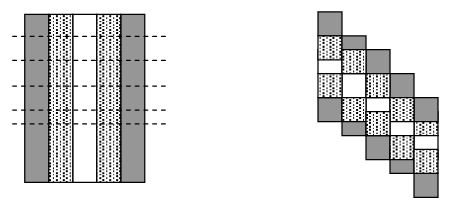
Suorakulmio on monen tilkkutyömallin perusta. Suorakulmioita ommellaan
ensin yhteen ja tämän jälkeen saatu iso suorakulmio leikataan suorakul-
mioiksi, neliöiksi, suunnikkaiksi tai kolmioiksi. Näin saadaan monimut-
kaisiakin malleja koottu helposti. Esimerkki. Suorakulmioita ommellaan
ensin yhteen ja sitten leikataan saatu isompi suorakulmio pieniksi suora-
kulmioiksi(ks. kuva). Kun saatuja suorakulmioita siirretään neliöitä kierre-
tään eri asentoihin ja sitten ommellaan yhteen, saadaan pienistä suora-
kulmioista koostuva kuvio. Tätä intiaanien vaatteiden kuvioinnissa käytet-
tyä tekniikkaa kutsutaan Seminole -tekniikaksi.
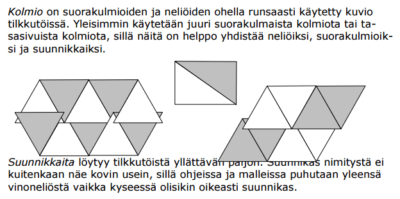
Kolmio on suorakulmioiden ja neliöiden ohella runsaasti käytetty kuvio
tilkkutöissä. Yleisimmin käytetään juuri suorakulmaista kolmiota tai ta-
sasivuista kolmiota, sillä näitä on helppo yhdistää neliöiksi, suorakulmioik-
si ja suunnikkaiksi.
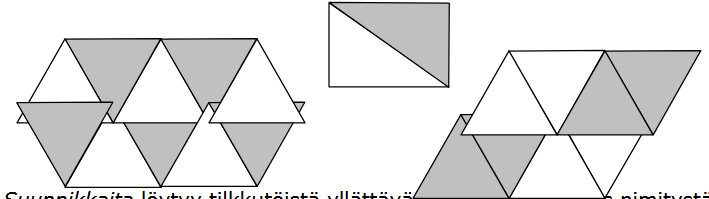
Suunnikkaita löytyy tilkkutöistä yllättävän paljon. Suunnikas nimitystä ei
kuitenkaan näe kovin usein, sillä ohjeissa ja malleissa puhutaan yleensä
vinoneliöstä vaikka kyseessä olisikin oikeasti suunnikas.
Säännöllisistä monikulmioista tutuimmat ovat viisi- ja kuusikulmio, joita
käytetään tilkkutöissä. Kun säännöllisiä viisikulmioita yhdistellään, saa-
daan pallomainen kappale. Kuusikulmioita yhdisteltäessä taas saadaan
aikaan taso. Tekstiilityön oppikirjassa on neuvottu kuinka piirretään viisi-
kulmio, mutta kuusikulmion piirtämistä ei ole neuvottu. (Karhu 1996,
208). Oppilaille joutuukin neuvomaan molempien monikulmioiden piirtä-
mistekniikan ja saattaa vielä joutua selittämäänkin minkä vuoksi viisikul-
mioista tulee kolmiulotteinen kappale ja kuusikulmioista taso.
Ympyrät toistuvat harvemmin tekstiilitöissä, mutta täysin vieras muoto
sekään ei ole. Jokainen oppilas on luultavasti tehnyt jossain vaiheessa pal-
lon muotoisen lankatupsun. Lankatupsu tehdään kiertämällä lankaa pahvi-
sen renkaan ympärille. Kun langat leikataan renkaan ulkoreunan kohdalta,
saadaan aikaan pallo, koska jokainen tupsussa oleva langanpätkä on pah-
visen ympyrän halkaisijan pituinen.
Vastaavanlaisia esimerkkejä löytyisi varmasti vaikka kuinka paljon ja tilk-
kutöiden maailma on aivan oma luokkaansa geometrian suhteen. Itsekin
kokee aina välillä ahaa-elämyksiä, kun oikein rupeaa miettimään, mitä
kaikkia geometrisia kuvioit yhdestä tilkkuyöstä voikaan löytää.
4 Ongelmanratkaisutaidot
Käsitöiden tekeminen vaatii jatkuvaa päättelyä ja arviointia. Työtä suunni-
teltaessa on pääteltävä, mikä on järkevä työjärjestys sujuvan työn teke-
misen kannalta. Jokaisessa tekniikassa on tiettyjä asioita jotka täytyy teh-
dä ennen muita vaiheita. Oppilas joutuukin monesti itse päättelemään,
mikä työvaihe kannattaa tehdä ensimmäisenä ja mikä viimeisenä. Tätä
päättelyä on monesti tehtävä läpi koko prosessin, sillä käsillä tehtäessä
kaikki ei mene aina niin kuin on suunniteltu.
Käsityön tekeminen on kuin suuren jatkuvan ongelman ratkaisemista. On-
gelmanratkaisuun oppilas törmää usein jo uutta työtä suunniteltaessa.
Oppilaalla on monesti mielikuva, mitä hän haluaa tehdä, mutta hänen täy-
tyy miettiä, kuinka se on hänen taidoillaan mahdollista. Koska oppilas ha-
luaa tehdä juuri sellaista tuotetta millainen mielikuva hänellä on, ei tuot-
teelle aina ole valmista mallia. Tällöin toteuttamista suunniteltaessa oppi-
las joutuu pohtimaan ja miettimään eri ratkaisuvaihtoehtojen sopivuutta.
Monesti oppilas joutuu myös aiemmin opittujen tietojen lisäksi etsimään
myös uutta tietoa. (Seppälä 1995, 70).
Lähteet
Karhu, P., Malmström, M. & Mannila, T. 1996. Hyvä Sauma. Tekstiilityön
käsikirja. Keuruu: Otava.
POPS 1996. Peruskoulun opetussuunnitelman perusteet 1994. Opetushalli-
tus. Helsinki: Edita Oy.
Seppälä, R. (toim.) 1994. Matematiikka – taitoa ajatella. Yläaste ja lukio.
Opetushallitus. Jyväskylä: Gummerus Kirjapaino Oy.
Seppälä, R. (toim.) 1995. Toimi, laske ja ajattele. Ala-aste. Opetushalli-
tus. Jyväskylä: Gummerus Kirjapaino Oy.
Matematiikkaa tekstiilityön tunnilla »