3-ulotteiset kappaleet
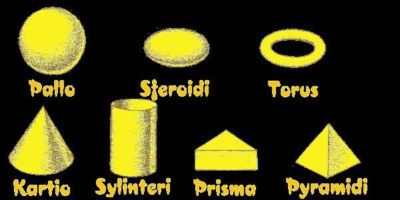
Kolmiulotteisilla kappaleilla on pinta-ala, tilavuus ja syvyys.
Syvyys on se ominaisuus, joka erottaa ne kaksiulotteisista geometrisista kuvioista. Kappaleita, jotka muodostuvat tasaisista pinnoista, sanotaan monitahokkaiksi. Sellaisten kappaleiden nimet, joissa on kaarevia pintoja, määräytyvät kaarevan muodon mukaan.
Säännölliset (Platonin) kappaleet
Kappaletta sanotaan säännölliseksi, jos sen pinta muodostuu tason osista, jotka ovat yhteneviä säännöllisiä monikulmioita.
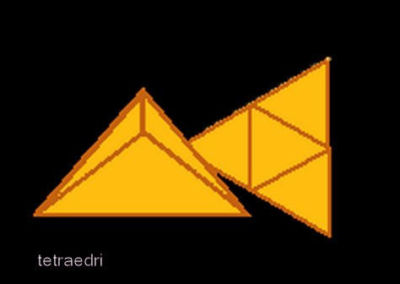
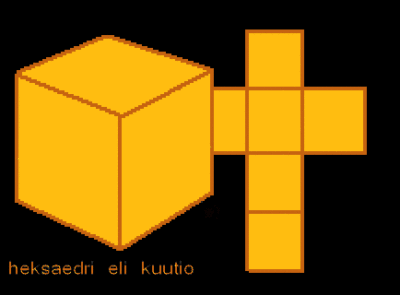
On olemassa vain viisi säännöllistä kappaletta, ja niistä kolmen pinta muodostuu tasasivuisista kolmioista.
Alla piirrokset säännöllisistä kappaleista, ja niissä käy myös ilmi, miten ne voidaan tehdä leikkaamalla ja taittelemalla pahvista.
 |
 |
 |
Ks. Platonin monitahokkaita (kaavoja) ja ompelua – matematiikkaa ja tekstiilityötä |
Puolisäännölliset (Arkhimedeen) kappaleet
Puolisäännöllisten kappaleiden pinta muodostuu useammanlaisista monikulmioista.
Esimerkiksi typistetyn tetraedrin pinta muodostuu tasasivuisista kolmioista ja 6-kulmioista.
Typistetyssä ikosaedrissa (huom. jalkapallossakin) on 12 viisi- ja 20 kuusikulmiota. Kuten säännölliset kappaleet, puolisäännöllisetkin kappaleet sopivat täsmälleen pallon sisälle eli kärjet koskettavat sen kuorta.
Kaikissa kappaleissa, joissa on tasapintaiset säännölliset tahkot, särmien lukumäärä on yhtä suuri kuin tahkojen lukumäärä plus kärkien lukumäärä miinus kaksi.
Esimerkiksi kuutio-oktaedrissa on 12 kärkeä ja 14 tahkoa, ja näin ollen siinä on 24 särmää.
Klikkaa kuvia, saat ne pyörimään!
Kun sisä- ja ulkopuoli ovat yhtä
Kaksi kappaletta, jotka muodostetaan yhdistämällä sylinterin päät:
1] Jos sylinterin päät (a) yhdistetään tavallisella tavalla, syntyy torus (b), koska päät yhtyessään ovat vastakkain.
2] Kleinin pullossa sylinterin (a) molempien päiden täytyy yhtyessään olla samansuuntaiset. Se tapahtuu siten, että toinen pää työnnetään sylinterin (b) seinämän läpi ja liitetään sitten ulkopuolelta toiseen päähän. Tässä erikoislaatuisessa kappaleessa on vain yksi ainut pinta, eikä siis ole sisä- eikä ulkopuolta.
Tekijät: Kaksi 8. luokan tyttöä
Puolalanmäen koulu, Turku 2001